چکیده
این مقاله به بررسی جامع مفهوم گرادیان در مغناطیس، با تمرکز بر تغییرات مکانی میدان مغناطیسی (B) و اشاره به پتانسیل برداری مغناطیسی (A)، می‌پردازد. ابتدا، بنیان‌های نظری میدان‌های مغناطیسی، پتانسیل برداری مغناطیسی و تعریف ریاضی گرادیان مورد بحث قرار می‌گیرد. سپس، تحلیل ریاضی گرادیان‌های میدان مغناطیسی، شامل نمایش تانسوری آن، با تکیه بر معادلات ماکسول و روش‌های محاسبه ارائه می‌شود. در نهایت، کاربردهای گسترده مهندسی این مفهوم، از جمله در تصویربرداری تشدید مغناطیسی (MRI)، سیستم‌های ناوبری، جداسازی مغناطیسی، و نیروهای وارد بر دوقطبی‌های مغناطیسی و ذرات در پلاسما، تشریح می‌گردد. هدف این مقاله ارائه یک دیدگاه یکپارچه و عمیق از اهمیت گرادیان‌های مغناطیسی در علوم و مهندسی است.
مقدمه: چرا مطالعه گرادیان‌های مغناطیسی مهم است؟
مغناطیس، یکی از نیروهای بنیادی طبیعت، نقش حیاتی در پدیده‌های فیزیکی و کاربردهای فناورانه ایفا می‌کند. در حالی که خود میدان مغناطیسی اهمیت زیادی دارد، تغییرات فضایی آن، که تحت عنوان گرادیان میدان مغناطیسی شناخته می‌شود، و همچنین تغییرات مکانی پتانسیل برداری مغناطیسی (A)، در بسیاری از کاربردهای پیشرفته مهندسی و پزشکی کلیدی هستند. درک و کنترل دقیق این گرادیان‌ها امکان توسعه فناوری‌های نوینی را فراهم آورده است.
تعریف اولیه و اهمیت گرادیان مغناطیسی
گرادیان یک کمیت فیزیکی، نرخ تغییرات مکانی آن کمیت را نشان می‌دهد. در حوزه مغناطیس، عمدتاً با گرادیان میدان مغناطیسی (B) و گاهی با گرادیان یا مشتقات فضایی پتانسیل برداری مغناطیسی (A) سروکار داریم. گرادیان میدان مغناطیسی مشخص می‌کند که میدان مغناطیسی با چه سرعتی و در چه جهتی در فضا تغییر می‌کند. این تغییرات می‌تواند در شدت یا جهت میدان مغناطیسی باشد. اهمیت گرادیان مغناطیسی از آنجا ناشی می‌شود که نیروهای مغناطیسی وارد بر مواد مغناطیسی و دوقطبی‌ها، ولتاژهای القایی در رساناها، و پدیده‌هایی مانند رانش ذرات باردار در پلاسما، نه تنها به خود میدان، بلکه به گرادیان آن نیز وابسته هستند.
اهداف مقاله
مقاله حاضر با هدف ارائه یک مرور جامع بر جنبه‌های مختلف گرادیان‌های مغناطیسی تدوین شده است. اهداف اصلی این مقاله عبارتند از:
- ارائه مبانی نظری میدان‌های مغناطیسی، پتانسیل برداری مغناطیسی و مفهوم گرادیان.
- تحلیل ریاضی دقیق گرادیان‌های میدان مغناطیسی، شامل نمایش تانسوری آن، و چگونگی محاسبه آن‌ها.
- بررسی کاربردهای عملی و مهندسی گرادیان‌های مغناطیسی در صنایع مختلف، با تاکید بر نیروهای ناشی از گرادیان.
- برجسته ساختن اهمیت تحقیقات در این حوزه برای پیشرفت‌های آینده.
ساختار مقاله
این مقاله در سه بخش اصلی سازماندهی شده است. بخش اول به مبانی نظری گرادیان مغناطیسی می‌پردازد. بخش دوم به تحلیل ریاضی و روش‌های محاسبه اختصاص دارد. بخش سوم کاربردهای مهندسی این مفهوم را مورد بررسی قرار می‌دهد. در نهایت، یک جمع‌بندی از نکات کلیدی و چشم‌اندازهای آتی ارائه خواهد شد.
بدنه اصلی: مبانی نظری، تحلیل ریاضی و کاربردها
مبانی نظری گرادیان مغناطیسی
برای درک گرادیان مغناطیسی، ابتدا باید با مفاهیم پایه میدان مغناطیسی، پتانسیل برداری مغناطیسی و عملگر گرادیان آشنا شویم.
میدان مغناطیسی و بردار چگالی شار مغناطیسی
میدان مغناطیسی، فضایی است که در آن نیروهای مغناطیسی قابل تشخیص هستند. این میدان توسط بارهای الکتریکی در حال حرکت (جریان‌های الکتریکی) یا مواد مغناطیسی (مانند آهنرباهای دائمی) ایجاد می‌شود. کمیت اصلی برای توصیف میدان مغناطیسی، بردار چگالی شار مغناطیسی است که با نماد B نشان داده می‌شود و واحد آن تسلا (T) است. B یک بردار است، یعنی علاوه بر اندازه، جهت نیز دارد.
مثلاً، در یک سیستم مختصات کارتزین، بردار B را می‌توان به صورت زیر نوشت:
که در آن Bx,By,Bz مؤلفه‌های میدان در راستای محورهای x,y,z و i^,j^,k^ بردارهای یکه متناظر هستند.
پتانسیل برداری مغناطیسی (A) و ارتباط آن با میدان B
در الکترومغناطیس، اغلب راحت‌تر است که میدان مغناطیسی B را از طریق یک پتانسیل برداری مغناطیسی A تعریف کنیم. این دو کمیت با رابطه زیر به هم مرتبط می‌شوند:
که در آن 
عملگر کرل است. پتانسیل برداری A یکتا نیست و می‌توان گرادیان هر تابع اسکالر دلخواهی را به آن افزود (پیمانه) بدون آنکه میدان B تغییر کند. تغییرات مکانی A نیز در تحلیل‌های پیشرفته الکترومغناطیس، به ویژه در مکانیک کوانتومی و نظریه میدان، اهمیت دارد.
تعریف ریاضی عملگر گرادیان
عملگر گرادیان، که با نماد ∇ (نَبلا) نشان داده می‌شود، یک عملگر برداری دیفرانسیلی است. وقتی این عملگر بر روی یک تابع اسکالر (مانند دما یا پتانسیل) اعمال می‌شود، برداری را نتیجه می‌دهد که جهت بیشترین نرخ افزایش آن تابع و اندازه آن نرخ افزایش را نشان می‌دهد. برای یک تابع اسکالر f(x,y,z)، گرادیان به صورت زیر تعریف می‌شود:
در اینجا، ∂x∂f مشتق جزئی تابع f نسبت به متغیر x است.
گرادیان میدان مغناطیسی (∇B) و مؤلفه‌های آن
مفهوم “گرادیان میدان مغناطیسی” می‌تواند به چند صورت تفسیر شود. اگر منظور گرادیان هر یک از مؤلفه‌های اسکالر میدان مغناطیسی باشد (مثلاً گرادیان Bx)، آنگاه تعریف بالا مستقیماً قابل استفاده است.
اما به طور کلی‌تر، گرادیان یک میدان برداری مانند B یک تانسور مرتبه دو است که نرخ تغییرات هر مؤلفه میدان B را در هر یک از جهات فضایی نشان می‌دهد. این تانسور (که گاهی ژاکوبین میدان برداری نیز نامیده می‌شود) به صورت زیر نمایش داده می‌شود:
[
\nabla \mathbf{B} = \begin{pmatrix}
<6>frac{\partial B_x}{\partial x} & \frac{\partial B_x}{\partial y} & \frac{\partial B_x}{\partial z} \
\frac{\partial B_y}{\partial x} & \frac{\partial B_y}{\partial y} & \frac{\partial B_y}{\partial z} \
\frac{\partial B_z}{\partial x} & \frac{\partial B_z}{\partial y} & \frac{\partial B_z}{\partial z}
\end{pmatrix}
]
این ۹ مؤلفه ∂xj∂Bi (که i,j می‌توانند x,y,z باشند) برای تحلیل دقیق نیروهای مغناطیسی در میدان‌های غیر یکنواخت و پدیده‌هایی مانند رانش ذرات در پلاسما ضروری هستند.
تحلیل ریاضی گرادیان‌های مغناطیسی
تحلیل ریاضی گرادیان‌ها برای طراحی و بهینه‌سازی دستگاه‌هایی که از آن‌ها استفاده می‌کنند، ضروری است.
معادلات ماکسول و ارتباط با گرادیان
رفتار میدان‌های الکتریکی و مغناطیسی توسط مجموعه‌ای از چهار معادله به نام معادلات ماکسول توصیف می‌شود. دو معادله از این چهار معادله که به طور مستقیم با ویژگی‌های فضایی میدان مغناطیسی سروکار دارند عبارتند از:
- قانون گاوس برای مغناطیس:
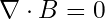این معادله بیان می‌کند که میدان مغناطیسی دیورژانس ندارد. - قانون آمپر-ماکسول:
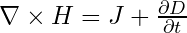(که در آن H شدت میدان مغناطیسی، J چگالی جریان الکتریکی و D جابجایی الکتریکی است). کرل (∇×) میدان مغناطیسی به جریان‌های الکتریکی و تغییرات زمانی میدان الکتریکی مرتبط است. همانطور که پیشتر ذکر شد، با استفاده از پتانسیل برداری A و با توجه به اینکه دیورژانس کرل هر برداری صفر است (
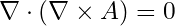), قانون گاوس برای مغناطیس به طور خودکار ارضا می‌شود.
محاسبه گرادیان در سیستم‌های مختصات مختلف
(محتوای این بخش بدون تغییر باقی می‌ماند)
روش‌های عددی برای محاسبه گرادیان
(محتوای این بخش بدون تغییر باقی می‌ماند)
کاربردهای مهندسی گرادیان مغناطیسی
گرادیان‌های مغناطیسی در طیف وسیعی از فناوری‌ها و کاربردهای مهندسی نقش اساسی دارند.
نیروی ناشی از گرادیان میدان بر مواد و دوقطبی‌های مغناطیسی
یکی از مهم‌ترین پیامدهای وجود گرادیان در میدان مغناطیسی، ایجاد نیرو بر روی مواد مغناطیسی و دوقطبی‌های مغناطیسی است. برای یک دوقطبی مغناطیسی با گشتاور مغناطیسی μ که در یک میدان مغناطیسی B قرار دارد، انرژی پتانسیل آن U=−μ⋅B است. نیروی وارد بر این دوقطبی از منفی گرادیان انرژی پتانسیل به دست می‌آید:
این فرمول کلی است. اگر گشتاور دوقطبی μ مستقل از میدان باشد (مانند یک آهنربای دائمی کوچک یا یک ذره بنیادی)، و جهت آن نیز ثابت باشد، می‌توان نیرو را بر حسب مؤلفه‌های گرادیان میدان نوشت. به عنوان یک حالت خاص مهم، اگر گشتاور دوقطبی μ همسو با میدان B باشد (یا در راستای آن قفل شده باشد)، نیرو تمایل دارد دوقطبی را به سمت مناطقی با شدت میدان ∣B∣ بیشتر حرکت دهد. این اصل اساس بسیاری از کاربردهای جداسازی مغناطیسی است.
تصویربرداری تشدید مغناطیسی (MRI)
(محتوای این بخش با تاکید بر اینکه گرادیان‌ها برای کدگذاری فضایی سیگنال‌ها استفاده می‌شوند، مشابه مقاله اولیه باقی می‌ماند و با اطلاعات مقاله کوتاه شما همخوانی دارد).
سیستم‌های ناوبری و موقعیت‌یابی مغناطیسی
(محتوای این بخش بدون تغییر باقی می‌ماند)
جداسازی مغناطیسی و تمرکز ذرات
همانطور که در بخش نیروی ناشی از گرادیان میدان توضیح داده شد، نیروی وارد بر یک ذره مغناطیسی در یک میدان مغناطیسی غیر یکنواخت، امکان جداسازی و تمرکز این ذرات را فراهم می‌کند. از این اصل در جداسازی مغناطیسی مواد استفاده می‌شود. به عنوان مثال:
- در صنایع معدنی برای جداسازی کانی‌های مغناطیسی از باطله.
- در زیست‌فناوری برای جداسازی سلول‌ها یا مولکول‌های نشاندار شده با نانوذرات مغناطیسی.
- در تصفیه آب برای حذف آلاینده‌های مغناطیسی. با طراحی مناسب گرادیان‌های میدان، می‌توان ذرات را با دقت بالا جدا یا متمرکز کرد.
سنجش غیرمخرب (Non-Destructive Testing – NDT)
(محتوای این بخش بدون تغییر باقی می‌ماند)
ذخیره‌سازی داده‌های مغناطیسی
(محتوای این بخش بدون تغییر باقی می‌ماند)
سایر کاربردها
علاوه بر موارد فوق، گرادیان‌های مغناطیسی در حوزه‌های دیگری نیز کاربرد دارند، از جمله:
- شتاب‌دهنده‌های ذرات: برای متمرکز کردن و هدایت باریکه‌های ذرات باردار. گرادیان‌های میدان در آهنرباهای چهارقطبی (quadrupole magnets) برای ایجاد نیروهای کانونی استفاده می‌شوند.
- مهار پلاسما در تحقیقات همجوشی هسته‌ای (توکامک‌ها و استلراتورها): گرادیان‌های پیچیده میدان برای محصور کردن پلاسمای داغ استفاده می‌شوند. گرادیان میدان B (همراه با انحنای خطوط میدان) منجر به رانش‌های ذرات باردار (مانند رانش
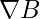و رانش انحنا) می‌شود که باید برای پایداری پلاسما به دقت کنترل شوند. این همان “نیروهای ناهمگنی” است که به آن اشاره شد. - بلبرینگ‌های مغناطیسی: برای تعلیق بدون تماس اجسام دوار و کاهش اصطکاک.
- سیستم‌های دارورسانی هدفمند: استفاده از نانوذرات مغناطیسی که توسط گرادیان‌های خارجی به سمت بافت هدف هدایت می‌شوند.
جمع‌بندی: خلاصه‌ای از یافته‌ها و چشم‌انداز آینده
مروری بر نکات کلیدی
این مقاله نشان داد که گرادیان میدان مغناطیسی، و به طور کلی‌تر تغییرات مکانی کمیت‌های مغناطیسی، مفهومی فراتر از یک تعریف ریاضی صرف بوده و دارای اهمیت بنیادی در علوم و مهندسی است. نکات کلیدی مطرح شده عبارتند از:
- گرادیان، نرخ و جهت تغییرات مکانی میدان مغناطیسی (و پتانسیل برداری آن) را توصیف می‌کند. گرادیان میدان برداری B یک تانسور است.
- تحلیل ریاضی گرادیان‌ها، مبتنی بر معادلات ماکسول و محاسبات دیفرانسیلی، برای درک رفتار آن‌ها ضروری است.
- نیروی وارد بر دوقطبی‌های مغناطیسی مستقیماً با گرادیان میدان مرتبط است (
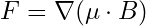). - کاربردهای مهندسی گرادیان‌های مغناطیسی بسیار متنوع و گسترده بوده و از پزشکی (MRI) تا صنایع سنگین (NDT) و تحقیقات پیشرفته (فیزیک پلاسما) را در بر می‌گیرد.
- فناوری‌هایی مانند MRI، NDT، جداسازی مغناطیسی و ذخیره‌سازی مغناطیسی به شدت به توانایی تولید، کنترل و اندازه‌گیری دقیق گرادیان‌های مغناطیسی وابسته‌اند.
چالش‌ها و تحقیقات آتی
(محتوای این بخش بدون تغییر عمده باقی می‌ماند، اما با درک عمیق‌تر از نیروها و تانسورها، می‌توان به چالش‌های دقیق‌تری در طراحی سیم‌پیچ‌های گرادیان برای دستیابی به پروفایل‌های خاص تانسور گرادیان اشاره کرد.)
منابع
(در یک مقاله واقعی، این بخش شامل لیستی از منابع مورد استناد خواهد بود.)
مثال:
- Griffiths, D. J. (2017). Introduction to Electrodynamics. Cambridge University Press.
- Jackson, J. D. (1999). Classical Electrodynamics. John Wiley & Sons.1
- Haacke, E. M., Brown, R. W., Thompson, M. R., & Venkatesan, R. (1999). Magnetic Resonance Imaging: Physical Principles and Sequence Design. Wiley-Liss.2
امیدوارم اکنون ساختار تیترها کاملاً مطابق با دستورالعمل و استاندارد باشد. باز هم از دقت نظر شما متشکرم.