Yörünge Mekaniği ve Yörünge Hesaplamaları

Yorum bırakın • 2. Havacılıkta Matematiğin Rolü, Gebra Blog • Yazan• 49 Views

2. Havacılıkta Matematiğin Rolü Gebra Blog

Yörünge Mekaniği ve Uzay Araçlarının Hareketi

Uzayda hareketin incelenmesinde matematiksel modellerin rolü büyüktür. Yörünge mekaniği, bir cismi belirli bir yol boyunca hareket ettiren kuvvetlerin analizini içerir. Uzay araçlarının doğru bir şekilde yörüngelere yerleştirilmesi ve yönlendirilmesi için matematiksel hesaplamalar gereklidir. Bu hesaplamalar, hem gezegenler arası seyahatlerde hem de uydu yerleştirme görevlerinde kullanılır.

Yörünge mekaniği, Newton’un çekim yasası ve Kepler’in hareket yasaları gibi temel fiziksel ilkelere dayanır. Bu yazıda, yörünge mekaniği ile ilgili önemli matematiksel formüller ve hesaplama yöntemleri ele alınacaktır.

Yörünge Mekaniği: Temel Matematiksel İlkeler

Yörünge mekaniğinde kullanılan en temel formüllerden biri, Newton’un evrensel çekim yasasıdır. Bu yasa, iki cisim arasındaki çekim kuvvetini şöyle ifade eder:

F = G \cdot \frac{m_1 m_2}{r^2}

Burada:

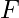  • F çekim kuvveti,
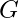  • G evrensel çekim sabiti,
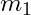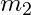  • m_1 ve m_2 iki cisim arasındaki kütleler,
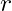  • r ise iki cisim arasındaki mesafedir.

Bu formül, yörüngedeki cisimlerin hareketini belirlerken, cisimlerin birbirleriyle nasıl etkileştiğini hesaplamak için kullanılır.

Yörünge Hesaplamaları

Bir uzay aracının yörüngede nasıl hareket ettiğini anlamak için, yörüngesel hız ve yörünge yarıçapı gibi temel parametrelerin hesaplanması gereklidir. Bu hesaplamalar için kullanılan temel formüller şunlardır:

  • Yörünge Hızı (Orbital Velocity):

v = \sqrt{\frac{GM}{r}}

Burada:

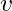  • v yörünge hızı,
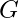  • G evrensel çekim sabiti,
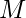  • M yörüngede hareket eden büyük cismi (örneğin, Dünya veya Güneş),
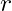  • r yörünge yarıçapıdır.

Yörünge hızını doğru hesaplamak, uzay araçlarının yörüngelere yerleştirilmesi ve doğru rotalarda hareket etmesi için oldukça önemlidir.

Yörünge Hesaplamalarında Zaman

Yörüngedeki bir cismin yörüngede ne kadar süreyle hareket edeceğini belirlemek için Kepler’in üçüncü yasası kullanılır. Kepler’in yasasına göre, yörünge dönemi T ile yörünge yarıçapı r arasında şu ilişki bulunur:

T^2 = \frac{4\pi^2 r^3}{GM}

Burada:

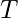  • T yörünge dönemi (zaman),
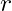  • r yörünge yarıçapı,
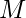  • M yörüngede hareket eden büyük cisim (örneğin, Dünya),
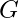  • G evrensel çekim sabiti.

Bu formül, özellikle uzay görevlerinin planlanmasında ve yörüngedeki zaman hesaplamalarında kullanılır.

Yörünge Hedeflemeleri ve Yerçekimi Yardımcı Manevralar

Yerçekimi yardımlı manevralar (gravitational assists) kullanılarak, bir uzay aracı bir gezegenin çekim kuvvetinden yararlanarak hız kazanabilir. Bu manevra, şu formüle göre hesaplanabilir:

\Delta v = 2 \cdot \frac{V_{\text{planet}} \cdot \sin(\theta)}{r}

Burada:

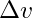  • \Delta v hız değişimi,
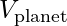  • V_{\text{planet}} gezegenin hızı,
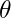  • \theta uzay aracı ve gezegen arasındaki açı,
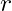  • r gezegenin yörünge yarıçapıdır.

Bu tür manevralar, uzay araçlarının hızlarını artırarak, görevlerin daha kısa sürede ve daha verimli bir şekilde tamamlanmasını sağlar.

Örnek: Bir Uyduyu Yörüngede Hız Hesaplama

Diyelim ki, Dünya etrafında dönen bir uyduya sahibiz ve bu uydunun yörünge hızını hesaplamak istiyoruz. Uydu, Dünya’nın yüzeyinden 500 kilometre yükseklikte dairesel bir yörüngede hareket ediyor. Yörünge hızını bulmak için, yörünge hızı için kullanılan formülü kullanabiliriz:

v = \sqrt{\frac{GM}{r}}

Burada:

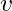  • v uyduyun yörünge hızı,
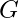  • G evrensel çekim sabiti (6.674 \times 10^{-11} , \text{m}^3 , \text{kg}^{-1} , \text{s}^{-2}),
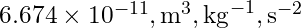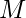  • M Dünya’nın kütlesi (5.972 \times 10^{24} , \text{kg}),
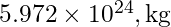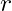  • r Dünya’nın merkezine olan uzaklıktır.

Adım Adım Hesaplama:

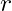  1. Mesafe r‘yi Belirleyin:
    Dünya’nın yarıçapı yaklaşık 6,371 km ve uydu, Dünya yüzeyinden 500 km yüksekliktedir. Bu nedenle, Dünya’nın merkezine olan toplam mesafe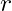 r şöyle hesaplanır: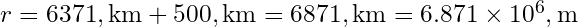 r = 6371 , \text{km} + 500 , \text{km} = 6871 , \text{km} = 6.871 \times 10^6 , \text{m}
  2. Değerleri Yörünge Hızı Formülüne Yerleştirin:
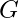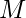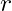    Şimdi, G, M ve r değerlerini yörünge hızı formülüne yerine koyabiliriz: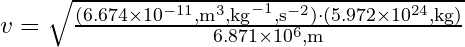 v = \sqrt{\frac{(6.674 \times 10^{-11} , \text{m}^3 , \text{kg}^{-1} , \text{s}^{-2}) \cdot (5.972 \times 10^{24} , \text{kg})}{6.871 \times 10^6 , \text{m}}}
  3. Basitleştirip Yörünge Hızını Hesaplayın:
    Şimdi ifadeyi basitleştirelim: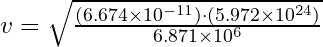 v = \sqrt{\frac{(6.674 \times 10^{-11}) \cdot (5.972 \times 10^{24})}{6.871 \times 10^6}} Bu şu şekilde basitleşir: 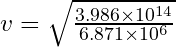v = \sqrt{\frac{3.986 \times 10^{14}}{6.871 \times 10^6}} Son olarak, yörünge hızını hesaplıyoruz: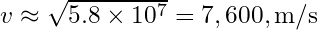 v \approx \sqrt{5.8 \times 10^7} = 7,600 , \text{m/s}

Böylece, uydunun yörünge hızı yaklaşık olarak 7,600 , \text{m/s} olarak bulunur.

Yorum ve puanlarınızla Gebra ekibinin kaliteyi artırmasına yardımcı olun

E-posta adresiniz yayınlanmayacak. Gerekli alanlar * ile işaretlenmişlerdir

Alışveriş Sepeti
Scroll to Top