Uçak ve Uzay Aracı Tasarımında Hesaplamalı Modelleme • GebraMS

Hesaplamalı Modelleme ve Uçak Tasarımı

Hesaplamalı modelleme, havacılık ve uzay mühendisliğinde, özellikle uçak ve uzay aracı tasarımı için kritik bir rol oynamaktadır. Bu modelleme, fiziksel süreçlerin matematiksel modelleri kullanılarak simüle edilmesiyle, gerçek dünya koşullarında nasıl performans gösterecekleri tahmin edilir. Bu süreçler, aerodinamik analizler, yapısal mühendislik, ısı transferi ve itki sistemlerinin tasarımı gibi alanlarda kullanılır.

Hesaplamalı modelleme, matematiksel denklemlerle birbirine bağlı fiziksel süreçleri temsil eder ve bu denklemler bilgisayarlar tarafından çözülerek mühendislik tasarımlarını optimize etmek için kullanılır.

Uçak ve Uzay Aracı Tasarımında Temel Hesaplamalı Modelleme Yöntemleri

Uçak ve uzay aracı tasarımında yaygın olarak kullanılan hesaplamalı modelleme yöntemlerinden bazıları şunlardır:

Aerodinamik simülasyonlar: Uçuşun verimliliğini ve güvenliğini optimize etmek için uçak kanatlarının çevresindeki hava akışının modellenmesi.
Yapısal modelleme: Malzeme gerilmeleri, bükülmeleri ve deforme olma süreçlerinin simülasyonu.
Isı transferi simülasyonları: Uçakların dış yüzeylerinde ve uzay araçlarının geri giriş süreçlerinde ısıyı nasıl yöneteceklerinin hesaplanması.
İtki sistemleri modelleme: Motorlar ve itki sistemlerinin aerodinamik ve termodinamik performanslarının analiz edilmesi.

Bu modelleme işlemleri, genellikle bilgisayarla simülasyon (Computational Fluid Dynamics, CFD) yazılımları kullanılarak gerçekleştirilir.

Aerodinamik Hesaplamalar ve Navier-Stokes Denklemleri

Havacılık ve uzay mühendisliğinde aerodinamik performansı belirlemek için genellikle Navier-Stokes denklemleri kullanılır. Bu denklemler, akışkanların hareketini ve buna bağlı olarak uçak kanadındaki hava akışını hesaplamak için temel matematiksel modeldir. Akışkanlar dinamiği için kullanılan temel denklemlerden biri Navier-Stokes denklemidir:

$\rho \left( \frac{\partial \mathbf{v}}{\partial t} + \mathbf{v} \cdot \nabla \mathbf{v} \right) = -\nabla p + \mu \nabla^2 \mathbf{v} + \mathbf{f}$

Burada:

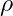$\rho$ : Akışkanın yoğunluğu,
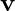$\mathbf{v}$ : Akışkanın hız vektörü,
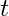$t$ : Zaman,
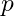$p$ : Basınç,
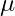$\mu$ : Dinamik viskozite,
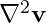$\nabla^2 \mathbf{v}$ : Hızın ikinci türevi (akışkanın viskozitesinin etkisi),
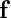$\mathbf{f}$ : Dış kuvvetler (örneğin yerçekimi).

Bu denklem, akışkanın hareketine etki eden tüm kuvvetleri içermektedir ve özellikle aerodinamik tasarımlarda kanatların etrafındaki hava akışının modellenmesinde kullanılır.

Yapısal Modelleme ve Malzeme Gerilmesi

Uçak ve uzay aracı tasarımında, yapıların dayanıklılığını değerlendirmek için yapısal modelleme teknikleri kullanılır. Bu modelleme, malzemenin dayanıklılığı, bükülme, çekme ve gerilme gibi faktörleri hesaba katarak uçak kanatlarının, gövdesinin ve uzay aracı yapılarının güvenliğini sağlar.

Yapısal analizlerde kullanılan temel denklemler, Hooke Yasası gibi elastik denklemlerle başlar. Hooke Yasası şu şekilde ifade edilir:

$\sigma = E \cdot \epsilon$

Burada:

$\sigma$ : Gerilme,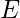
$E$ : Elastik modül (Young Modülü),
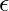$\epsilon$ : Birim uzama (deformasyon).

Bu formül, malzeme üzerinde uygulanan kuvvetlerin malzemenin deformasyonu üzerindeki etkisini hesaplamak için kullanılır.

Isı Transferi ve Termodinamik Simülasyonlar

Isı transferi simülasyonları, uçakların dış yüzeylerinde ve uzay araçlarının geri giriş (re-entry) süreçlerinde ısıyı nasıl yöneteceklerini belirlemek için önemlidir. Fourier’in Isı İletim Yasası, ısı akışını tanımlamak için kullanılan temel denklemlerden biridir:

$q = -k \cdot \nabla T$

Burada:

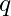$q$ : Isı akışı,
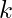$k$ : Isı iletkenliği (malzemenin ısıyı iletme yeteneği),
$\nabla T$ : Sıcaklık gradyanı.

Bu denklem, ısı transferini anlamak ve yapıların sıcaklık kontrolünü sağlamak için önemlidir.

İtki Sistemleri Modelleme

İtki sistemlerinin verimli çalışması, özellikle uzay araçlarında kritik öneme sahiptir. İtki sistemlerinde termodinamik döngüler ve gaz dinamiği hesaplamaları büyük rol oynar. Bir jet motoru için kullanılan isohorizantal termodinamik döngü şu şekilde hesaplanabilir:

$W = \dot{m} \cdot (h_2 - h_1)$

Burada:

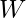$W$ : İş (veya güç),
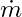$\dot{m}$ : Kütle akışı,
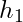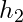$h_1$ ve $h_2$ : Akışkanın entalpileri (giriş ve çıkış).

Bu formül, bir motorun enerji verimliliğini ve performansını değerlendirmek için kullanılır.

Örnek: Bir Kanadın Etrafındaki Hava Akışının Hesaplanması

Diyelim ki bir uçak kanadının etrafındaki hava akışını hesaplamak istiyoruz. Uçak kanadının hava hızının $v = 100 , \text{m/s}$ olduğu ve kanat yüzeyinin $S = 20 , \text{m}^2$ olduğu varsayalım. Ayrıca, havanın yoğunluğu $\rho = 1.225 , \text{kg/m}^3$ ve dinamik viskozitesi $\mu = 1.81 \times 10^{-5} , \text{kg/(m⋅s)}$ olduğunu kabul edelim.

Adım Adım Çözüm:

Akışkanlar Dinamiği: Navier-Stokes Denklemi

Kanat etrafındaki hava akışını hesaplamak için, Navier-Stokes denklemlerini kullanacağız. Bu denklemler, akışkanların hareketini modellemek için en temel araçtır:

$\rho \left( \frac{\partial \mathbf{v}}{\partial t} + \mathbf{v} \cdot \nabla \mathbf{v} \right) = -\nabla p + \mu \nabla^2 \mathbf{v} + \mathbf{f}$

Burada:

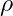$\rho$ : Akışkanın yoğunluğu,
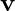$\mathbf{v}$ : Akışkanın hız vektörü,
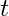$t$ : Zaman,
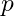$p$ : Basınç,
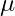$\mu$ : Dinamik viskozite,
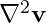$\nabla^2 \mathbf{v}$ : Hızın ikinci türevi (akışkanın viskozitesinin etkisi),
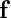$\mathbf{f}$ : Dış kuvvetler.

Bu denklem, akışkanın hızını ve basıncını hesaplayarak, kanat yüzeyinde ortaya çıkan hava akışını simüle eder.

Kanat Üzerindeki Hava Hızı ve Basınç Farkı

Uçak kanadındaki hava hızının farklı bölgelerde nasıl değiştiğini belirlemek için Bernoulli Prensibi‘ni uygulayabiliriz. Bernoulli Prensibi’ne göre, bir akışkanın hızı arttıkça basıncı düşer. Kanat üzerindeki hız farkı, basınç farkı yaratır. Bu fark, kaldırma kuvvetini oluşturur.

Bernoulli denklemi şu şekilde ifade edilebilir:

$P_{\text{top}} - P_{\text{alt}} = \frac{1}{2} \rho \left( v_{\text{alt}}^2 - v_{\text{top}}^2 \right)$

Burada:

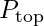$P_{\text{top}}$ : Kanadın üst yüzeyindeki basınç,
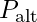$P_{\text{alt}}$ : Kanadın alt yüzeyindeki basınç,
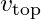$v_{\text{top}}$ : Kanat üst yüzeyindeki hava hızı,
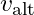$v_{\text{alt}}$ : Kanat alt yüzeyindeki hava hızı.

Varsayılan hava hızları:

$v_{\text{top}} = 100 , \text{m/s}$ ,
$v_{\text{alt}} = 90 , \text{m/s}$ .

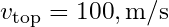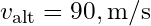Bu hız farkı, kanat üzerindeki basınç farkını hesaplamamıza olanak tanır.

Basınç Farkı Hesaplaması

Şimdi, hız farkını kullanarak basınç farkını hesaplayalım:

$P_{\text{top}} - P_{\text{alt}} = \frac{1}{2} \times 1.225 \times \left( (90)^2 - (100)^2 \right)$

$P_{\text{top}} - P_{\text{alt}} = \frac{1}{2} \times 1.225 \times \left( 8100 - 10000 \right)$

$P_{\text{top}} - P_{\text{alt}} = \frac{1}{2} \times 1.225 \times (-1900)$

$P_{\text{top}} - P_{\text{alt}} = -1167.5 , \text{Pa}$

Bu basınç farkı, kanadın üst yüzeyinin alt yüzeyinden daha düşük basınca sahip olduğunu gösteriyor ve bu fark, kanadın kaldırma kuvvetini oluşturur.

Kaldırma Kuvveti Hesaplaması

Kaldırma kuvvetini hesaplamak için basınç farkını kanat alanı ile çarpmamız gerekir. Kaldırma kuvveti şu şekilde hesaplanır:

$L = (P_{\text{top}} - P_{\text{alt}}) \times S$

$L = -1167.5 , \text{Pa} \times 20 , \text{m}^2$

$L = -23,350 , \text{N}$

Kaldırma kuvveti yukarı yönlü olduğu için büyüklüğünü alırız:

$L = 23,350 , \text{N}$

Sonuç olarak, kanat üzerindeki kaldırma kuvveti $23,350 , \text{N}$ ‘dir.

Reynolds Sayısı Hesaplaması

Şimdi, bu akışın Reynolds sayısını hesaplayalım. Reynolds sayısı, akışın türbülanslı mı yoksa laminer mi olduğunu belirlememize yardımcı olur.

Reynolds sayısı formülü:

$Re = \frac{\rho v L}{\mu}$

Burada:

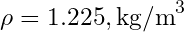$\rho = 1.225 , \text{kg/m}^3$ (hava yoğunluğu),
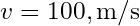$v = 100 , \text{m/s}$ (kanat üzerindeki hız),
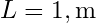$L = 1 , \text{m}$ (kanadın karakteristik uzunluğu),
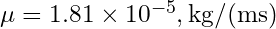$\mu = 1.81 \times 10^{-5} , \text{kg/(m⋅s)}$ (dinamik viskozite).

Reynolds sayısını hesaplayalım:

$Re = \frac{(1.225) \times (100) \times (1)}{(1.81 \times 10^{-5})}$

$Re = \frac{122.5}{1.81 \times 10^{-5}} = 6.77 \times 10^6$

Sonuç olarak, Reynolds sayısı yaklaşık olarak $6.77 \times 10^6$ ‘dır, bu da akışın turbülanslı olduğunu gösterir.

Sonuç

Hesaplamalardan:

Kanat üzerindeki kaldırma kuvveti yaklaşık olarak 23,350 N‘dir, bu da uçağın havada kalabilmesi için üretilen kuvveti gösterir.
Reynolds sayısı yaklaşık olarak 6.77 milyon‘dur, bu da akışın turbülanslı olduğunu ve akışın aerodinamik performansı ve sürüklemeyi etkileyebileceğini gösterir.

Bu örnek, akışkanlar dinamiğinin havacılık tasarımındaki önemini göstermektedir. Navier-Stokes denklemleri ve Bernoulli Prensibi gibi temel matematiksel kavramları kullanarak, uçak kanatlarının ve uzay araçlarının yüzeylerinin tasarımını optimize edebiliriz.

Hızlı Erişim	Önemli Bilgiler	İletişim
Anasayfa	Satış Sözleşmesi	info@gebrams.com
Hakkımızda	Kullanım Sözleşmesi
Sepetim	Gizlilik Ve Güvenlik
Fırsat Ürünler	İade ve Garanti
Tüm Ürünler	Ödeme Yöntemleri

Banka Hesaplarımız
İş Bankası
Garanti Bankası
Vakıf Bankası
Akbank

Şirket Adı	Gebra Mühendislik Sanayı LTD. ŞTİ

Hesaplamalı Modelleme ve Uçak Tasarımı

Uçak ve Uzay Aracı Tasarımında Temel Hesaplamalı Modelleme Yöntemleri

Aerodinamik Hesaplamalar ve Navier-Stokes Denklemleri

Yapısal Modelleme ve Malzeme Gerilmesi

Isı Transferi ve Termodinamik Simülasyonlar

İtki Sistemleri Modelleme

Örnek: Bir Kanadın Etrafındaki Hava Akışının Hesaplanması

Adım Adım Çözüm:

Akışkanlar Dinamiği: Navier-Stokes Denklemi

Kanat Üzerindeki Hava Hızı ve Basınç Farkı

Basınç Farkı Hesaplaması

Kaldırma Kuvveti Hesaplaması

Reynolds Sayısı Hesaplaması

Sonuç

Yorum ve puanlarınızla Gebra ekibinin kaliteyi artırmasına yardımcı olun Yanıtı iptal et