چکیده
این مقاله به بررسی جامع و پیشرفته مفهوم گرادیان در مغناطیس میپردازد. با تمرکز بر دو کمیت اساسی، میدان مغناطیسی ![]() و پتانسیل برداری مغناطیسی
و پتانسیل برداری مغناطیسی ![]() , روابط ریاضی و فیزیکی گرادیان این کمیتها به صورت تانسوری تحلیل شدهاند. کاربردهای گسترده و جزئیات فنی این مفهوم در فناوریهای نوین از جمله تصویربرداری تشدید مغناطیسی (MRI)، سیستمهای کنترل پلاسما، و **میکروسکوپ نیروی مغناطیسی (MFM)** به تفصیل مورد بحث قرار گرفتهاند. همچنین، روشهای محاسباتی و چالشهای عملی در این حوزه بررسی میشوند.
, روابط ریاضی و فیزیکی گرادیان این کمیتها به صورت تانسوری تحلیل شدهاند. کاربردهای گسترده و جزئیات فنی این مفهوم در فناوریهای نوین از جمله تصویربرداری تشدید مغناطیسی (MRI)، سیستمهای کنترل پلاسما، و **میکروسکوپ نیروی مغناطیسی (MFM)** به تفصیل مورد بحث قرار گرفتهاند. همچنین، روشهای محاسباتی و چالشهای عملی در این حوزه بررسی میشوند.
### مقدمه: مبانی و اهمیت گرادیان در پدیدههای مغناطیسی
گرادیان در مغناطیس به تغییرات مکانی کمیتهای برداری یا اسکالر مغناطیسی اشاره دارد. این تغییرات مکانی، منشأ بسیاری از پدیدههای فیزیکی مهم و اساس کارکرد دستگاههای فناورانه متعدد است. در این مقاله، ما عمدتاً بر دو نوع گرادیان تمرکز خواهیم کرد:
* **گرادیان میدان مغناطیسی (![]() ):** که تغییرات فضایی پتانسیلی را نشان میدهد که میدان مغناطیسی از آن مشتق میشود.
):** که تغییرات فضایی پتانسیلی را نشان میدهد که میدان مغناطیسی از آن مشتق میشود.
درک این مفاهیم در شاخههای مختلف فیزیک، از جمله الکترومغناطیس، فیزیک پلاسما، فیزیک ماده چگال، و همچنین در رشتههای مهندسی برق و مهندسی پزشکی، از اهمیت ویژهای برخوردار است.
اهداف و ساختار مقاله
هدف این مقاله، ارائه یک تحلیل عمیق از مبانی نظری گرادیانهای مغناطیسی، فرمولبندی ریاضی دقیق آنها، بررسی نیروهای ناشی از این گرادیانها، و کاربردهای پیشرفته آنها در فناوری است. همچنین، به روشهای عددی مورد استفاده برای محاسبه این گرادیانها و چالشهای موجود در این زمینه پرداخته خواهد شد.
مقاله به این ترتیب سازمان یافته است: ابتدا مبانی نظری و تعاریف ریاضی گرادیان ![]() و
و ![]() ارائه میشود. سپس نیروهای ناشی از گرادیانها، به ویژه نیروی وارد بر دوقطبی مغناطیسی، تحلیل میگردد. در ادامه، کاربردهای کلیدی شامل MRI، کنترل پلاسما و MFM بررسی میشوند. پس از آن، مروری بر روشهای محاسباتی و چالشها و محدودیتهای عملی خواهیم داشت و در نهایت، مقاله با یک نتیجهگیری به پایان میرسد.
ارائه میشود. سپس نیروهای ناشی از گرادیانها، به ویژه نیروی وارد بر دوقطبی مغناطیسی، تحلیل میگردد. در ادامه، کاربردهای کلیدی شامل MRI، کنترل پلاسما و MFM بررسی میشوند. پس از آن، مروری بر روشهای محاسباتی و چالشها و محدودیتهای عملی خواهیم داشت و در نهایت، مقاله با یک نتیجهگیری به پایان میرسد.
بدنه اصلی: تحلیل نظری، ریاضی و کاربردهای پیشرفته
مبانی نظری و تعاریف ریاضی
میدان مغناطیسی (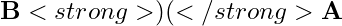 )
)
میدان مغناطیسی ![]() یک میدان برداری است که اثرات مغناطیسی نیروهای الکترومغناطیسی را توصیف میکند. این میدان را میتوان از پتانسیل برداری مغناطیسی
یک میدان برداری است که اثرات مغناطیسی نیروهای الکترومغناطیسی را توصیف میکند. این میدان را میتوان از پتانسیل برداری مغناطیسی ![]() به صورت زیر به دست آورد:
به صورت زیر به دست آورد:
![]()
این رابطه یکی از معادلات بنیادین ماکسول، یعنی ![]() (عدم وجود تکقطبی مغناطیسی)، را به طور خودکار ارضا میکند.
(عدم وجود تکقطبی مغناطیسی)، را به طور خودکار ارضا میکند.
گرادیان میدان مغناطیسی ( )
)
گرادیان میدان مغناطیسی ![]() یک تانسور مرتبه دوم است که ۹ مؤلفه آن، نرخ تغییرات هر یک از مؤلفههای
یک تانسور مرتبه دوم است که ۹ مؤلفه آن، نرخ تغییرات هر یک از مؤلفههای ![]() را در هر یک از جهات
را در هر یک از جهات ![]() نشان میدهد:
نشان میدهد:
[
\nabla \mathbf{B} =
\begin{pmatrix}
<9>frac{\partial B_x}{\partial x} & \frac{\partial B_x}{\partial y} & \frac{\partial B_x}{\partial z} \
\frac{\partial B_y}{\partial x} & \frac{\partial B_y}{\partial y} & \frac{\partial B_y}{\partial z} \
\frac{\partial B_z}{\partial x} & \frac{\partial B_z}{\partial y} & \frac{\partial B_z}{\partial z}
\end{pmatrix}
]
هر عنصر این تانسور، مانند ![]() , نشان میدهد که مؤلفه z میدان چگونه با تغییر مکان در جهت x تغییر میکند. این تانسور در تحلیل نیروهای دقیق و گشتاورهای وارد بر اجسام مغناطیسی در میدانهای غیر یکنواخت اهمیت دارد.
, نشان میدهد که مؤلفه z میدان چگونه با تغییر مکان در جهت x تغییر میکند. این تانسور در تحلیل نیروهای دقیق و گشتاورهای وارد بر اجسام مغناطیسی در میدانهای غیر یکنواخت اهمیت دارد.
گرادیان پتانسیل برداری مغناطیسی (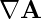 )
)
به طور مشابه، گرادیان پتانسیل برداری ![]() نیز یک تانسور مرتبه دوم است:
نیز یک تانسور مرتبه دوم است:
[
\nabla \mathbf{A} =
\begin{pmatrix}
<10>frac{\partial A_x}{\partial x} & \frac{\partial A_x}{\partial y} & \frac{\partial A_x}{\partial z} \
\frac{\partial A_y}{\partial x} & \frac{\partial A_y}{\partial y} & \frac{\partial A_y}{\partial z} \
\frac{\partial A_z}{\partial x} & \frac{\partial A_z}{\partial y} & \frac{\partial A_z}{\partial z}
\end{pmatrix}
]
گرچه ![]() به طور مستقیم در بسیاری از فرمولهای فیزیکی رایج ظاهر نمیشود، اما در فرمولبندیهای پیشرفتهتر نظریه میدان و در تحلیلهای پیمانهای خاص میتواند مورد استفاده قرار گیرد. مشتقات
به طور مستقیم در بسیاری از فرمولهای فیزیکی رایج ظاهر نمیشود، اما در فرمولبندیهای پیشرفتهتر نظریه میدان و در تحلیلهای پیمانهای خاص میتواند مورد استفاده قرار گیرد. مشتقات ![]() در محاسبه
در محاسبه ![]() نقش اساسی دارند.
نقش اساسی دارند.
نیروهای ناشی از گرادیانهای مغناطیسی
انرژی پتانسیل دوقطبی مغناطیسی
انرژی پتانسیل ![]() یک دوقطبی مغناطیسی با گشتاور دوقطبی
یک دوقطبی مغناطیسی با گشتاور دوقطبی ![]() در یک میدان مغناطیسی خارجی
در یک میدان مغناطیسی خارجی ![]() به صورت زیر تعریف میشود:
به صورت زیر تعریف میشود:
![]()
این انرژی به جهتگیری نسبی دوقطبی و میدان بستگی دارد.
نیروی وارد بر دوقطبی مغناطیسی
نیروی ![]() وارد بر یک دوقطبی مغناطیسی در یک میدان مغناطیسی از منفی گرادیان انرژی پتانسیل آن به دست میآید:
وارد بر یک دوقطبی مغناطیسی در یک میدان مغناطیسی از منفی گرادیان انرژی پتانسیل آن به دست میآید:
![]()
اگر گشتاور دوقطبی ![]() ثابت فرض شود (یعنی به میدان
ثابت فرض شود (یعنی به میدان ![]() یا مکان وابسته نباشد، که تقریب خوبی برای آهنرباهای دائمی کوچک یا ذرات بنیادی است)، این نیرو را میتوان به صورت زیر نیز نوشت:
یا مکان وابسته نباشد، که تقریب خوبی برای آهنرباهای دائمی کوچک یا ذرات بنیادی است)، این نیرو را میتوان به صورت زیر نیز نوشت:
![]()
در شرایطی که جریان آزاد در محل دوقطبی وجود نداشته باشد (![]() در آن نقطه)، یا اگر
در آن نقطه)، یا اگر ![]() موازی
موازی ![]() باشد، جمله دوم صفر شده و نیرو به صورت زیر ساده میشود:
باشد، جمله دوم صفر شده و نیرو به صورت زیر ساده میشود:
![]()
این فرم نشان میدهد که نیرو مستقیماً به مؤلفههای گرادیان ![]() و جهتگیری
و جهتگیری ![]() بستگی دارد. این نیرو اساس کار بسیاری از پدیدهها مانند جداسازی مغناطیسی و میکروسکوپی نیروی مغناطیسی است. اگر
بستگی دارد. این نیرو اساس کار بسیاری از پدیدهها مانند جداسازی مغناطیسی و میکروسکوپی نیروی مغناطیسی است. اگر ![]() همسو با
همسو با ![]() باشد، نیرو در جهت افزایش شدت میدان
باشد، نیرو در جهت افزایش شدت میدان ![]() خواهد بود.
خواهد بود.
کاربردهای پیشرفته گرادیانهای مغناطیسی
تصویربرداری تشدید مغناطیسی (MRI)
در MRI، از گرادیانهای میدان مغناطیسی دقیق و کنترلشده برای کدگذاری فضایی سیگنالهای تشدید مغناطیسی هستهای استفاده میشود. سه گرادیان خطی و مستقل، معمولاً ![]() , به میدان مغناطیسی اصلی و یکنواخت
, به میدان مغناطیسی اصلی و یکنواخت ![]() (که معمولاً در جهت z است) اضافه میشوند:
(که معمولاً در جهت z است) اضافه میشوند:
![]()
این گرادیانها باعث میشوند فرکانس لارمور پروتونها (عمدتاً هیدروژن در آب و چربی) به مکان آنها وابسته شود:
![]()
که در آن ![]() نسبت ژیرومغناطیسی،
نسبت ژیرومغناطیسی، ![]() میدان اصلی،
میدان اصلی، ![]() بردار گرادیان اعمالی، و
بردار گرادیان اعمالی، و ![]() بردار مکان است. با کنترل دقیق این گرادیانها در طول زمان، میتوان تصاویر سهبعدی با وضوح بالا از داخل بدن ایجاد کرد.
بردار مکان است. با کنترل دقیق این گرادیانها در طول زمان، میتوان تصاویر سهبعدی با وضوح بالا از داخل بدن ایجاد کرد.
کنترل پلاسما در همجوشی هستهای
در دستگاههای همجوشی مغناطیسی مانند توکامکها و استلراتورها، میدانهای مغناطیسی قوی و پیچیده برای محصور کردن پلاسمای بسیار داغ (با دمای میلیونها درجه) به کار میروند. تعادل پایدار پلاسما توسط رابطه اساسی مگنتوهیدرودینامیک (MHD) توصیف میشود:
![]()
این معادله بیان میکند که گرادیان فشار پلاسما (![]() ) که
) که ![]() چگالی جریان در پلاسما است، موازنه شود. طراحی دقیق گرادیانهای میدان
چگالی جریان در پلاسما است، موازنه شود. طراحی دقیق گرادیانهای میدان ![]() برای دستیابی به این تعادل و پایداری طولانیمدت پلاسما حیاتی است.
برای دستیابی به این تعادل و پایداری طولانیمدت پلاسما حیاتی است.
میکروسکوپ نیروی مغناطیسی (MFM)
MFM یک نوع میکروسکوپ پراب پویشی است که برای تصویربرداری از ساختارهای مغناطیسی سطوح با قدرت تفکیک نانومتری استفاده میشود. نوک (tip) مغناطیسی شده میکروسکوپ، سطح نمونه را پویش میکند. نیروی مغناطیسی بین نوک و نمونه، که به گرادیان میدان مغناطیسی نمونه وابسته است، اندازهگیری میشود. اگر گشتاور مغناطیسی نوک ![]() و میدان مغناطیسی نمونه
و میدان مغناطیسی نمونه ![]() باشد، نیروی وارد بر نوک (به ویژه مؤلفه عمودی آن
باشد، نیروی وارد بر نوک (به ویژه مؤلفه عمودی آن ![]() ) معمولاً به صورت زیر تقریب زده میشود:
) معمولاً به صورت زیر تقریب زده میشود:
![]()
این تکنیک برای مطالعه دامنههای مغناطیسی در مواد فرومغناطیس، ابررساناها و سایر مواد مغناطیسی کاربرد دارد.
روشهای محاسباتی برای گرادیانهای مغناطیسی
محاسبه تحلیلی میدانها و گرادیانهای مغناطیسی تنها برای هندسههای بسیار ساده امکانپذیر است. در مسائل عملی، از روشهای عددی استفاده میشود:
روش تفاضل محدود (Finite Difference Method – FDM)
در این روش، مشتقات با تقریبهای تفاضلی جایگزین میشوند. به عنوان مثال، مشتق جزئی ![]() نسبت به x را میتوان با استفاده از یک فرمول تفاضل مرکزی تقریب زد:
نسبت به x را میتوان با استفاده از یک فرمول تفاضل مرکزی تقریب زد:
![]()
این روش برای هندسههای منظم مناسب است اما پیادهسازی شرایط مرزی در هندسههای پیچیده میتواند دشوار باشد.
روش المان محدود (Finite Element Method – FEM)
FEM یک روش قدرتمند و انعطافپذیر برای حل معادلات دیفرانسیل جزئی در هندسههای پیچیده است. در مسائل مغناطیس ایستا، اغلب معادله پواسون برای پتانسیل برداری مغناطیسی ![]() حل میشود:
حل میشود:
![]()
که در آن ![]() تراوایی مغناطیسی خلأ و
تراوایی مغناطیسی خلأ و ![]() چگالی جریان آزاد است. پس از محاسبه
چگالی جریان آزاد است. پس از محاسبه ![]() در گرههای شبکه المان محدود، میدان
در گرههای شبکه المان محدود، میدان ![]() و سپس گرادیان
و سپس گرادیان ![]() به صورت عددی محاسبه میشوند. نرمافزارهای تجاری متعددی بر پایه FEM برای شبیهسازیهای الکترومغناطیسی وجود دارند.
به صورت عددی محاسبه میشوند. نرمافزارهای تجاری متعددی بر پایه FEM برای شبیهسازیهای الکترومغناطیسی وجود دارند.
چالشها و محدودیتها
در طراحی و استفاده از سیستمهای مبتنی بر گرادیان مغناطیسی، چندین چالش و محدودیت عملی وجود دارد:
- اثرات لبهای و غیرخطی بودن: در گرادیانهای عملی تولید شده توسط سیمپیچها، میدانها در لبههای سیمپیچها اغلب غیر یکنواخت هستند (اثرات لبهای). همچنین، وجود مواد فرومغناطیس میتواند منجر به رفتار غیرخطی شود.
- محدودیتهای گرمایی: تولید گرادیانهای مغناطیسی قوی، به ویژه در کاربردهایی مانند MRI که نیاز به سویچینگ سریع گرادیانها دارند، میتواند منجر به تولید گرمای قابل توجهی در سیمپیچهای گرادیان به دلیل مقاومت الکتریکی شود. این گرما باید به طور مؤثری دفع شود.
- دقت و پایداری عددی: شبیهسازی گرادیانهای پیچیده، به ویژه در نزدیکی منابع میدان یا در مرز مواد با خواص مغناطیسی متفاوت، میتواند از نظر عددی چالشبرانگیز باشد و نیاز به شبکهبندی دقیق و روشهای حل پایدار دارد.
- تداخل و نویز: میدانهای مغناطیسی خارجی و نویز الکترومغناطیسی میتوانند بر اندازهگیری و کنترل دقیق گرادیانها تأثیر بگذارند.
نتیجهگیری و چشمانداز آینده
گرادیان در مغناطیس، مفهومی بنیادین با پیامدهای گسترده در علوم و فناوری است. از توصیف نیروهای دقیق وارد بر مواد مغناطیسی گرفته تا امکان تصویربرداریهای پزشکی پیشرفته و کنترل پلاسمای داغ، درک و مهندسی گرادیانهای مغناطیسی نقش محوری ایفا میکند. پیشرفتها در مواد مغناطیسی جدید (مانند ابررساناهای دمای بالا برای تولید میدانهای قویتر)، الگوریتمهای محاسباتی کارآمدتر برای شبیهسازی دقیقتر، و تکنیکهای اندازهگیری حساستر، به طور مداوم مرزهای آنچه با استفاده از گرادیانهای مغناطیسی امکانپذیر است را گسترش میدهند. تحقیقات آینده احتمالاً بر روی سیستمهای گرادیان کوچکتر، قویتر، دقیقتر و با مصرف انرژی بهینهتر متمرکز خواهد شد و کاربردهای نوینی را در حوزههایی مانند نانوفناوری، علوم اعصاب و انرژی پاک آشکار خواهد ساخت.
منابع
(در یک مقاله کامل، این بخش شامل فهرست دقیقی از مراجع مورد استفاده خواهد بود. مثالهایی از مراجع کلیدی عبارتند از:)
- Jackson, J. D. (1999). Classical Electrodynamics (3rd ed.). Wiley.
- Griffiths, D. J. (2017). Introduction to Electrodynamics (4th ed.). Cambridge University Press.
- Haacke, E. M., Brown, R. W., Thompson, M. R., & Venkatesan, R. (1999). Magnetic Resonance Imaging: Physical Principles and Sequence Design. Wiley-Liss.1
- Chen, F. F. (2016). Introduction to Plasma Physics and Controlled Fusion (3rd ed.). Springer.
- Zangwill, A. (2013). Modern Electrodynamics. Cambridge University Press.