Akışkanlar Dinamiği ve Havacılıkta Uygulamaları
Akışkanlar dinamiği, bir akışkanın (hava, su vb.) hareketini inceleyen bilim dalıdır. Havacılık ve uzay mühendisliğinde, uçak ve uzay araçlarının tasarımı için akışkanlar dinamiği büyük bir öneme sahiptir. Bu alan, özellikle aerodinamik tasarımlar, itki sistemleri, ısı transferi ve yapıların dayanıklılığı için kritik hesaplamalar içerir. Uçakların havada süzülmesi ve uzay araçlarının atmosfer dışında hareket etmesi, akışkanlar dinamiği prensiplerine dayanır.
Bu yazıda, uçak ve uzay aracı tasarımında akışkanlar dinamiği ile ilgili temel matematiksel formüller ele alınacaktır. Matematiksel modellemeler, özellikle aerodinamik analizler, akışkanların davranışlarını tahmin etmemize ve mühendislik tasarımlarını optimize etmemize olanak sağlar.
Akışkanlar Dinamiği Temelleri
Akışkanlar dinamiği, Newton’un hareket yasalarına dayanarak akışkanların hareketini inceler. Bu, hız, basınç ve yoğunluk gibi parametrelerle ilişkili olan bir dizi denkleme dayanır. Akışkanların hareketi, temelde üç ana kuvvetle ilgilidir: basınç farkı, sürtünme ve yoğunluk farkı.
Bir akışkanın hareketini açıklamak için kullanılan temel denklemlerden biri Navier-Stokes denklemidir. Bu denklem, bir akışkanın hızını ve basıncını belirler:
![]()
Burada:
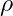 : Akışkanın yoğunluğu,
: Akışkanın yoğunluğu,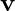 : Akışkanın hız vektörü,
: Akışkanın hız vektörü,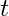 : Zaman,
: Zaman,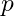 : Basınç,
: Basınç,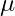 : Dinamik viskozite,
: Dinamik viskozite,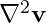 : Hızın ikinci türevi (akışkanın viskozitesinin etkisi),
: Hızın ikinci türevi (akışkanın viskozitesinin etkisi),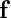 : Dış kuvvetler (örneğin yerçekimi).
: Dış kuvvetler (örneğin yerçekimi).
Bu denklem, akışkanın hareketine etki eden tüm kuvvetleri içermektedir. Havacılık ve uzay mühendisliğinde, bu denklem kullanılarak uçakların aerodinamik performansı ve uzay araçlarının tasarımı için gerekli hesaplamalar yapılır.
Uçak Tasarımında Akışkanlar Dinamiği
Uçakların tasarımında akışkanlar dinamiği, aerodinamik hesaplamaların temelini oluşturur. Uçak kanatlarının şekli, kanadın çevresindeki havanın nasıl hareket edeceğini belirler. Bu hareket, kanat üzerinde bir basınç farkı yaratır ve bu basınç farkı, uçağın havada kalmasını sağlayan kaldırma kuvvetini üretir.
Kanat profilindeki akışkanlar dinamiği, uçakların hızını, manevra kabiliyetini ve yakıt verimliliğini etkiler. Bu hesaplamalar için kullanılan başlıca denklemler arasında Bernoulli Prensibi yer alır.
Bernoulli Prensibi
Bernoulli prensibine göre, bir akışkanın hızının arttığı bölgelerde basınç azalır. Bu prensip, uçak kanatlarında kaldırma kuvveti üretmek için kritik bir rol oynar:
![]()
Burada:
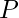 : Basınç,
: Basınç,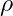 : Akışkanın yoğunluğu,
: Akışkanın yoğunluğu,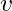 : Akışkanın hızı.
: Akışkanın hızı.
Kanat üzerindeki hız farkı, basınç farkına yol açar ve bu fark uçağın havada kalmasını sağlar. Bu prensip, uçak kanatları üzerinde hız farkları yaratılarak kaldırma kuvveti elde edilmesini sağlar.
Uzay Aracı Tasarımında Akışkanlar Dinamiği
Uzay araçlarının tasarımında da akışkanlar dinamiği büyük bir rol oynar, ancak bu kez farklı bir ortamda, yani uzayda veya atmosferin dışında çalışılır. Yüksek hızlarda uzay araçlarının atmosferdeki sürükleme kuvvetlerine karşı nasıl tepki vereceği, aerodinamik tasarımın en önemli unsurlarından biridir.
Uzay araçları, atmosferin dışına çıktıklarında, düşük yoğunluklu bir ortamda hareket ederler, ancak atmosferde iken, sürtünme kuvvetleri uçuş hızlarını sınırlandırabilir. Uzay aracının yüzey tasarımı, hava ile etkileşimde nasıl bir kuvvet oluşturulacağını belirler. Bu etkileşimler, ısı transferi, sürtünme ve hızlanma gibi faktörleri içerir.
Uzay aracının giriş hızını hesaplarken, Reynolds sayısı gibi bir parametre de hesaplanır. Reynolds sayısı, akışkanın viskozitesi ve hızına bağlı olarak, akışın laminer mi yoksa türbülanslı mı olacağını belirler.
![]()
Burada:
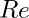 : Reynolds sayısı,
: Reynolds sayısı,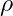 : Akışkanın yoğunluğu,
: Akışkanın yoğunluğu,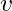 : Hız,
: Hız,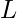 : Uzay aracının karakteristik uzunluğu,
: Uzay aracının karakteristik uzunluğu,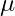 : Dinamik viskozite.
: Dinamik viskozite.
Örnek: Bir Kanat Üzerinde Kaldırma Kuvvetinin Hesaplanması
Diyelim ki, bir uçak kanadının üst yüzeyinde hava hızı ![]() , alt yüzeyinde ise
, alt yüzeyinde ise ![]() olsun. Hava yoğunluğu ise
olsun. Hava yoğunluğu ise ![]() (deniz seviyesi standart koşullarında) ve kanadın yüzeyi
(deniz seviyesi standart koşullarında) ve kanadın yüzeyi ![]() .
.
Bernoulli Prensibine göre, kanat üzerindeki hız farkı bir basınç farkı yaratır ve bu basınç farkı kaldırma kuvvetini oluşturur. Basınç farkını hesaplamak için şu formül kullanılır:
![]()
Burada:
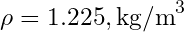 ,
,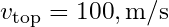 ,
,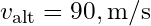 .
.
Adım Adım Çözüm:
- Basınç farkını hesaplayalım:
![]()
![]()
![]()
![]()
Bu negatif işaret, üst yüzeydeki basıncın alt yüzeydekinin daha düşük olduğunu gösterir.
- Kaldırma kuvvetini hesaplayalım:
Kaldırma kuvveti, basınç farkı ile kanat alanının çarpımıdır:
![]()
![]()
![]()
Kaldırma kuvveti yukarı yönlü olduğundan, büyüklüğünü alıyoruz:
![]()
Sonuç olarak, kanat üzerindeki kaldırma kuvveti yaklaşık olarak ![]() ‘dir.
‘dir.
Örnek: Reynolds Sayısını Hesaplama
Şimdi, aynı koşullar altında Reynolds sayısını hesaplayalım. Reynolds sayısı, akışın laminer mi yoksa türbülanslı mı olduğunu belirlemeye yardımcı olur.
Reynolds sayısı formülü:
![]()
Burada:
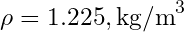 (hava yoğunluğu),
(hava yoğunluğu),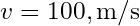 (kanat üzerindeki hava hızı),
(kanat üzerindeki hava hızı),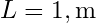 (kanadın karakteristik uzunluğu),
(kanadın karakteristik uzunluğu),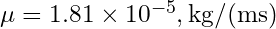 (havada dinamik viskozite).
(havada dinamik viskozite).
Adım Adım Çözüm:
- Değerleri yerine koyalım:
![]()
- Reynolds sayısını hesaplayalım:
![]()
Sonuç olarak, Reynolds sayısı yaklaşık olarak ![]() ‘dır ve bu da akışın turbülanslı olduğunu gösterir, çünkü Reynolds sayısı
‘dır ve bu da akışın turbülanslı olduğunu gösterir, çünkü Reynolds sayısı ![]() ‘in üzerindedir.
‘in üzerindedir.
Sonuç
Hesaplamalardan:
- Kanat üzerindeki kaldırma kuvveti yaklaşık olarak 23,350 N‘dir, bu da uçağın havada kalabilmesi için üretilen kuvveti gösterir.
- Reynolds sayısı yaklaşık olarak 6.77 milyon‘dur, bu da akışın turbülanslı olduğunu ve akışın aerodinamik performansı ve sürüklemeyi etkileyebileceğini gösterir.
Her iki örnek de akışkanlar dinamiğinin havacılık ve uzay tasarımındaki önemini vurgulamaktadır. Bernoulli Prensibi ve Reynolds sayısı gibi kavramları kullanarak, uçak kanatlarının ve uzay araçlarının yüzeylerinin tasarımını optimize edebiliriz.